A
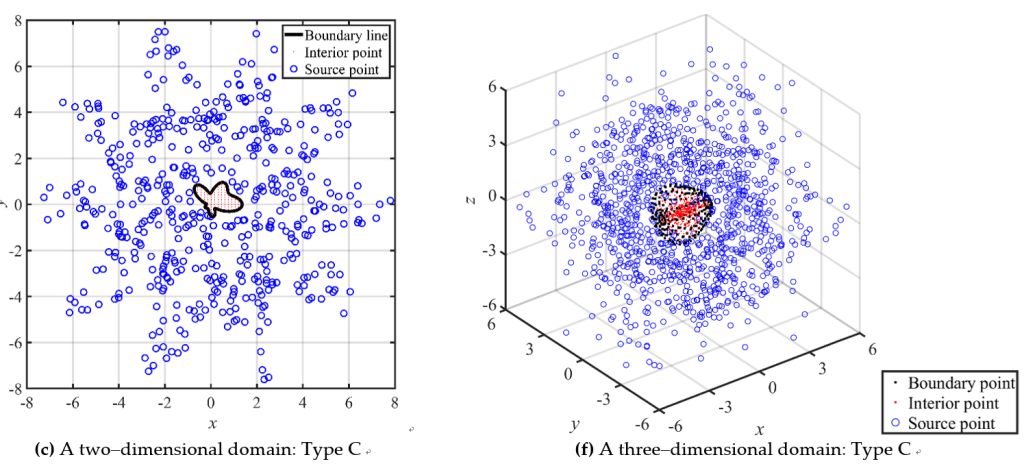
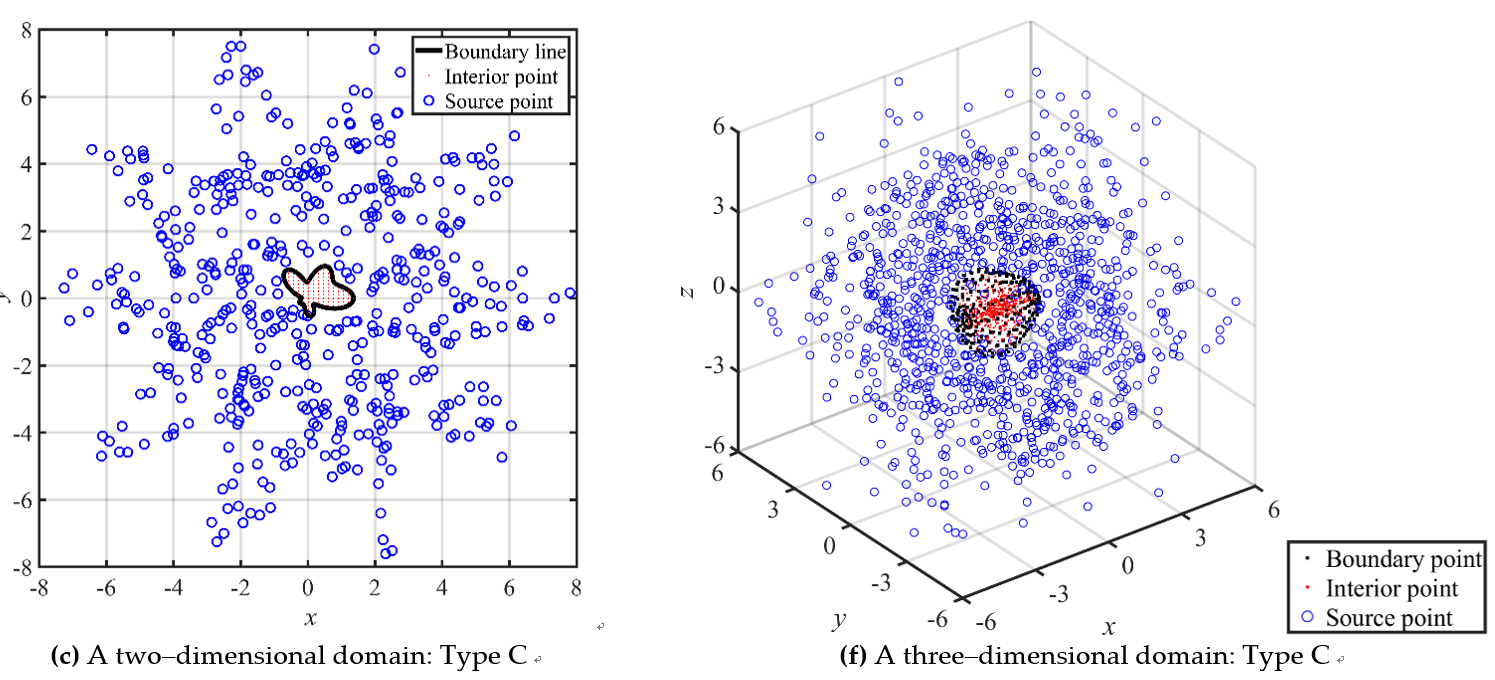
Abstract: In this article, we propose a simplified radial basis function (RBF) method with exterior fictitious sources for solving elliptic boundary value problems (BVPs). Three simplified RBFs including Gaussian, multiquadric (MQ), and inverse multiquadric (IMQ) without the shape parameter are adopted in this study. With the consideration of many exterior fictitious sources outside the domain, the radial distance of the RBF is always greater than zero such that we can remove the shape parameter from RBFs. Additionally, simplified Gaussian, MQ, and IMQ RBFs and their derivatives in the governing equation are always smooth and nonsingular. Comparative analysis is conducted for three different collocation types including conventional uniform centres, randomly fictitious centres, and exterior fictitious sources. Numerical examples of elliptic BVPs in two and three dimensions are carried out. Results demonstrate that the proposed simplified RBFs with exterior fictitious sources can significantly improve the accuracy, especially for the Laplace equation. Furthermore, the proposed simplified RBFs exhibit the simplicity of solving elliptic BVPs without finding the optimum shape parameter.
Keywords: radial basis function; the shape parameter; multiquadric; inverse multiquadric; Gaussian.
Abstract: https://www.mdpi.com/2227-7390/10/10/1622 PDF Version: https://www.mdpi.com/2227-7390/10/10/1622/pdf