Abstract: Elliptic boundary value problems (BVPs) are widely used in various scientific and engineering
disciplines that involve finding solutions to elliptic partial differential equations subject
to certain boundary conditions. This article introduces a novel approach for solving elliptic BVPs
using an artificial neural network (ANN)-based radial basis function (RBF) collocation method. In
this study, the backpropagation neural network is employed, enabling learning from training data
and enhancing accuracy. The training data consist of given boundary data from exact solutions
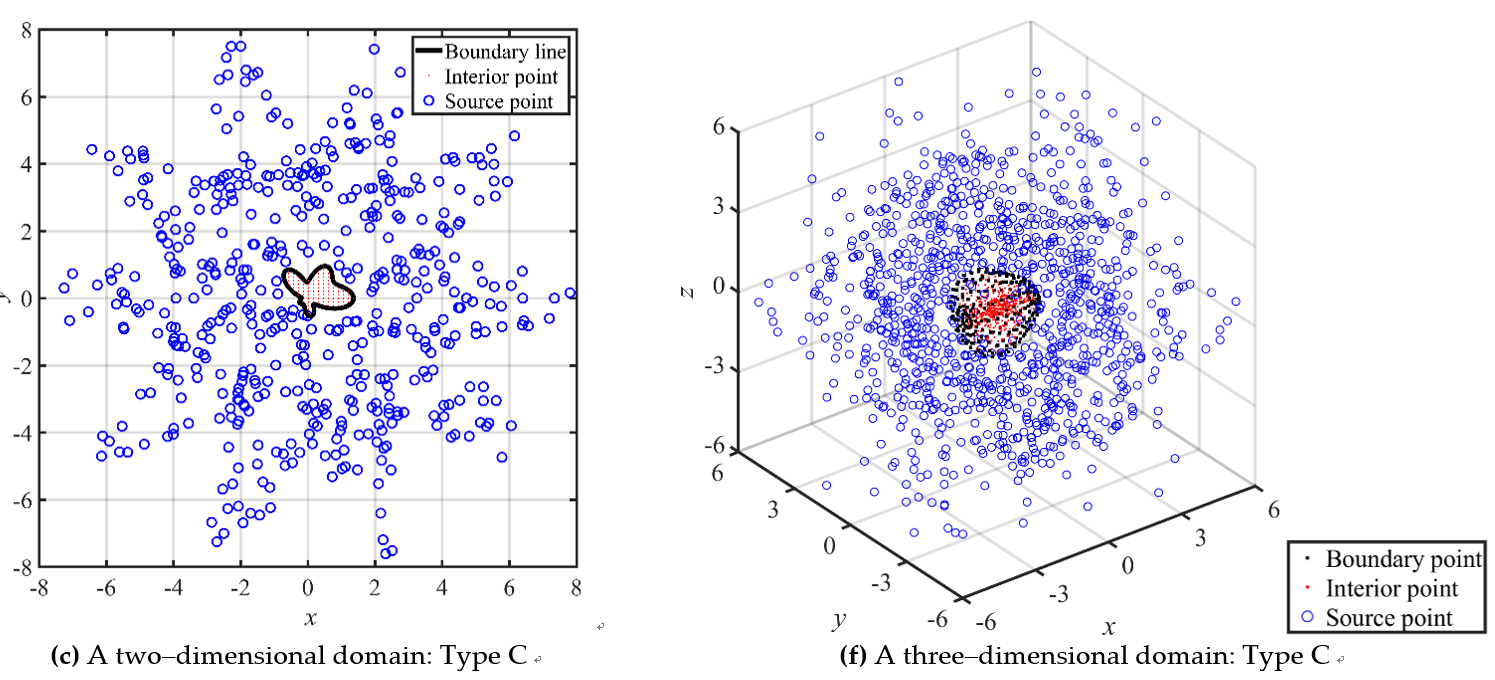
and the radial distances between exterior fictitious sources and boundary points, which are used to
construct RBFs, such as multiquadric and inverse multiquadric RBFs. The distinctive feature of this
approach is that it avoids the discretization of the governing equation of elliptic BVPs. Consequently,
the proposed ANN-based RBF collocation method offers simplicity in solving elliptic BVPs with
only given boundary data and RBFs. To validate the model, it is applied to solve two- and three dimensional elliptic BVPs. The results of the study highlight the effectiveness and efficiency of the
proposed method, demonstrating its capability to deliver accurate solutions with minimal data input
for solving elliptic BVPs while relying solely on given boundary data and RBFs.
Keywords: backpropagation neural network; radial basis function; boundary value problem;
multiquadric; collocation method
Paper download
https://doi.org/10.3390/math11183935
https://www.mdpi.com/2227-7390/11/18/3935