Mathematics 2024, 12(9), 1407;
https://doi.org/10.3390/math12091407
Abstract
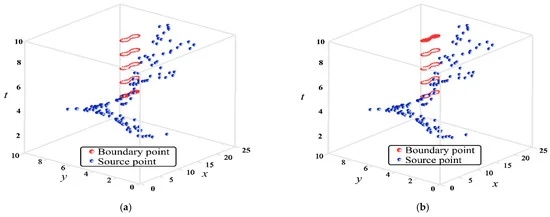
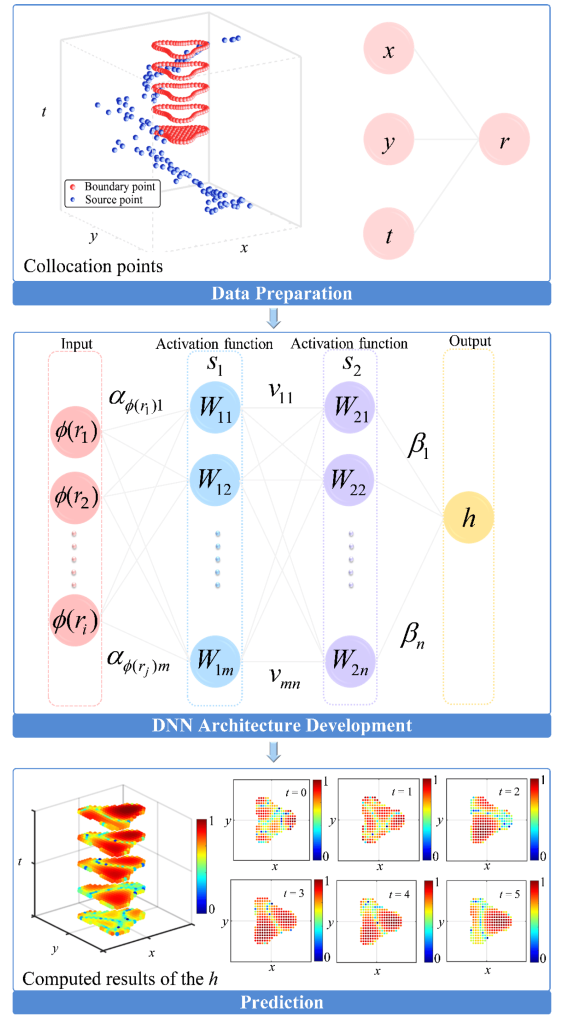
This study introduces a deep neural network approach that utilizes radial basis functions (RBFs) to solve forward and inverse problems in the process of diffusion. The input layer incorporates multiquadric (MQ) RBFs, symbolizing the radial distance between the boundary points on the spacetime boundary and the source points positioned outside the spacetime boundary. The output layer is the initial and boundary data given by analytical solutions of the diffusion equation. Utilizing the concept of the spacetime coordinates, the approximations for forward and backward diffusion problems involve assigning initial data on the bottom or top spacetime boundaries, respectively. As the need for discretization of the governing equation is eliminated, our straightforward approach uses only the provided boundary data and MQ RBFs. To validate the proposed method, various diffusion scenarios, including forward, backward, and inverse problems with noise, are examined. Results indicate that the method can achieve high-precision numerical solutions for solving diffusion problems. Notably, only 1/4 of the initial and boundary conditions are known, yet the method still yields precise results.
Keywords:
deep neural network; diffusion; multiquadric; radial basis function; spacetime