Abstract: Conventional methods for solving inverse wave problems struggle with illposedness,
significant computational demands, and discretization errors. In this study,
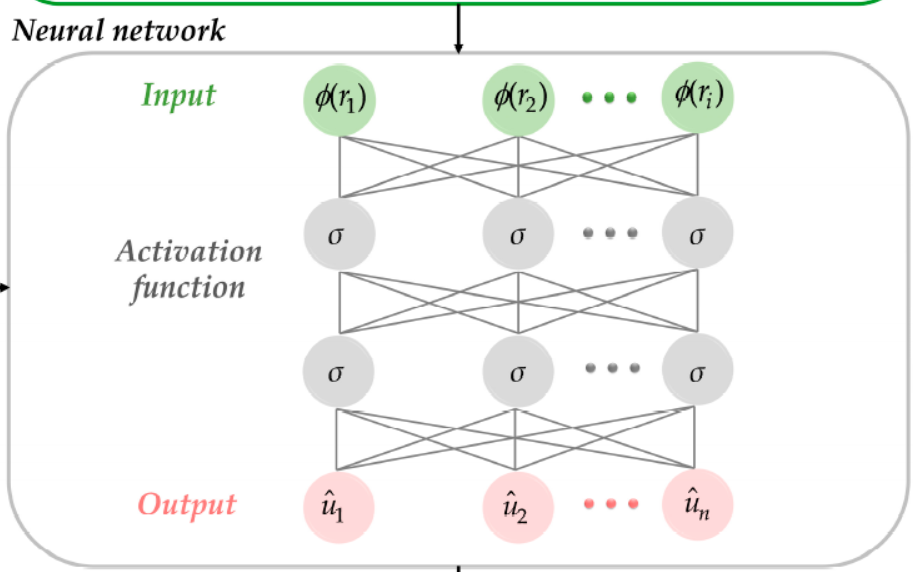
we propose an innovative framework for solving inverse problems in wave equations by
using deep learning techniques with spacetime radial basis functions (RBFs). The proposed
method capitalizes on the pattern recognition strength of deep neural networks (DNNs) and
the precision of spacetime RBFs in capturing spatiotemporal dynamics. By utilizing initial
conditions, boundary data, and radial distances to construct spacetime RBFs, this approach
circumvents the need for wave equation discretization. Notably, the model maintains
accuracy even with incomplete or noisy boundary data, illustrating its robustness and
offering significant advancements over traditional techniques in solving wave equations.
Keywords: inverse problems; wave equations; deep learning; physics-informed neural
networks; radial basis functions
MSC: 35D35; 65M3
Chih-Yu Liu, Cheng-Yu Ku*, Wei-Da Chen, Ying-Fan Lin and Jun-Hong Lin (2025), “Solving Inverse Wave Problems Using Spacetime Radial Basis Functions in Neural Networks,” Mathematics 2025, 13(5), 725, pp. 1-21. (SCIE, IF 2.3, Q1, 21/489 (4.3% JIF) in MATHEMATICS, JCR, 2023)
Full paper download can be accessed by the following link.
https://doi.org/10.3390/math13050725