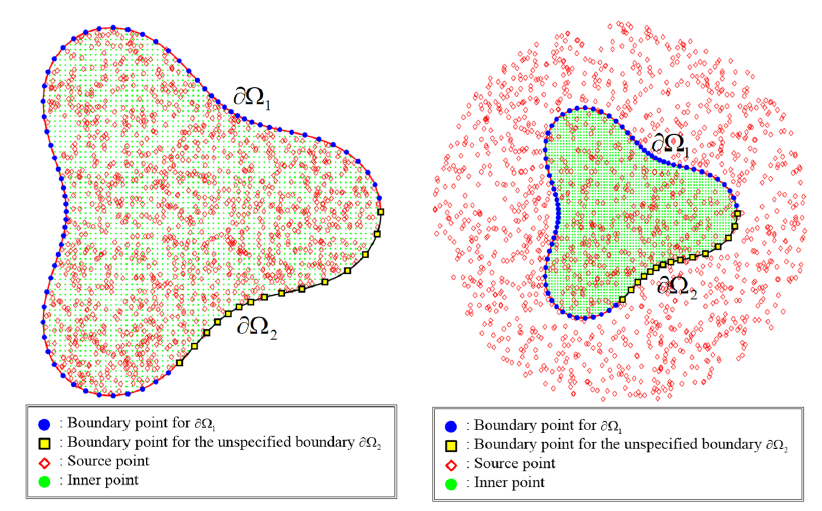
Abstract: In this article, the radial basis function method with polyharmonic polynomials for solving inverse problems of the stationary convection–diffusion equation is presented. We investigated the inverse problems in groundwater pollution problems for the multiply-connected domains containing a finite number of cavities. Using the given data on the part of the boundary with noises, we aim to recover the missing boundary observations, such as concentration on the remaining boundary or those of the cavities. Numerical solutions are approximated using polyharmonic polynomials instead of using the certain order of the polyharmonic radial basis function in the conventional polyharmonic spline at each source point. Additionally, highly accurate solutions can be obtained with the increase in the terms of the polyharmonic polynomials. Since the polyharmonic polynomials include only the radial functions. The proposed polyharmonic polynomials have the advantages of a simple mathematical expression, high precision, and easy implementation. The results depict that the proposed method could recover highly accurate solutions for inverse problems with cavities even with 5% noisy data. Moreover, the proposed method is meshless and collocation only such that we can solve the inverse problems with cavities with ease and efficiency.
Keywords: inverse problems; polyharmonic polynomials; radial basis function; groundwater
pollution; convection–diffusion
Download
https://doi.org/10.3390/app12094294